I want more Life

A teaser of where I’m headed, since there are a lot of words between here and the next image.

A few years ago, I was playing around with a variant on Conway’s Game of Life. My dissatisfaction with the standard version was that while it makes a fine substrate for machines, it doesn’t support dynamics that look like biological life.

Digression

If I had started down this path today, I would have realized I was letting my concern for what some arbitrary cellular automaton is called was getting in the way of appreciating what it is, or more precisely, what it does. I would have figured out that what I was looking for in Life was robustness. And it wasn’t even clear that it lacked this. The dynamics of life are fragile—flip a bit somewhere and the fanciest “spaceship” may fall apart—but there’s no mechanic within the system to expose this fragility. The true problem only manifests when you open up the system. Here’s one possible way to pin this down.

Suppose you turn the Game of Life into the Game of Life. Pick out some finite region of cells and call it “inside”; its complement is “outside”. The regions are controlled by players, respectively named Inside and Outside, who can set the initial states of their regions. Outside wins the game by putting “inside” into some prescribed state, say, all dead cells. If this does not happen in some prescribed (possibly infinite) number of steps, then Inside wins. There’s a lot of wiggle room here, but Inside winning maybe captures some of what I mean by robustness.

Digression ends

But back then, it felt like a very short and natural hop to go to from wanting to see biological dynamics to adding biologically-inspired mechanics. For concreteness, I called the resulting thing Lif.

For details on the dynamics I settled on, you can check out the repository for Lif on GitHub, where I put up a rough implementation. Here’s the gist, though:

• Each cell, alive or empty, has a stasis set containing the numbers of (alive) neighbors it can tolerate.
• At each step, cells with tolerable neighbors stay the same, and the rest flip state.
  • Newly empty cells start with a large stasis set, which shrinks over time.
  • Newly alive cells without neighbors (at the previous step) start with a small stasis set.
  • Newly alive cells with neighbors inherit their stasis set from a neighbor, with preference for a small stasis set and with the possibility of mutations.
• Alive cells occasionally change their stasis set towards consensus with a neighbor, with preference for neighbors of the same lineage and with the possibility of mutations.

(Exercise for reader: which stasis sets capture ordinary Life dynamics?)

The last part, a process that looks a lot like gene exchange, isn’t really that important except to prevent a stable/absorbing/boring monoculture of alive cells that can tolerate exactly eight neighbors. What ends up being most critical is how the stasis set of empty cells shrinks over time, which can be described as gain of habitability over time.

(Exercise for reader: think up a snappier name for “gain of habitability over time”.)

These rules encode a trade-off reminiscent of that in r/K selection: individuals that are better at settlement are worse at survival in varying conditions. It’s not a priori clear what this means for lineages, though.

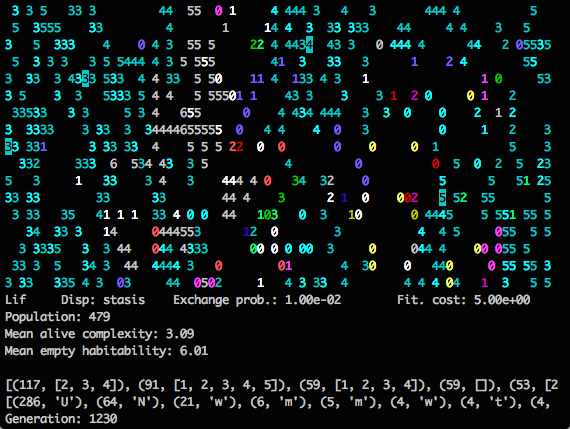
Gain of habitability through random removal from stasis set.

The above screenshot shows part of the full grid from a single time step in a run, with empty cells blank and alive cells showing the size of their stasis sets. Early in playing with Lif, I didn’t pay much attention to the gain of habitability mechanic, and these dynamics were unexciting. Random elements of empty cell stasis sets were removed, which meant that the stasis sets and configurations promoting effective settlement depended on particular empty area to be settled. This made extreme r-selected strategies unviable.

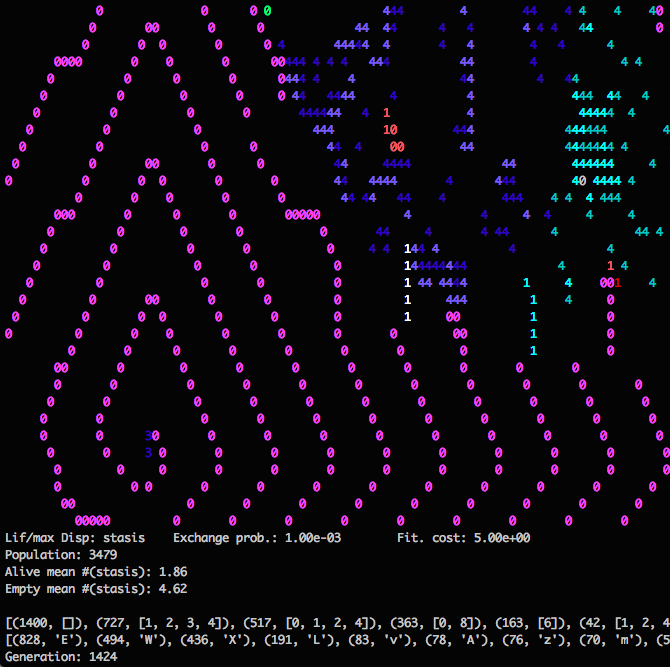
Gain of habitability through removal of largest number from stasis set.

Switching to removing the largest element from empty cell stasis sets opens up all sorts of cool new dynamics. There’s a lot going on here, but what has me excited about this variant is the spiral in the bottom-left. Spirals arise in this variant fairly naturally, and work defensively by resetting stasis sets to its largest value as waves of settlement arise and then die out. The unexpected part is the more complicated cells at the middle of the spiral. These cells, although not of the same lineage, are protected by and are themselves immune to the cells that they have come to organize.